CFD-FVM-03: Turbulence

What is turbulence

The velocity is decomposed into a steady mean value with a fluctuating component superimposed on it: . This is called the Reynolds decomposition. A turbulent flow can now be characterised in terms of the mean values of flow properties ( etc.) and some statistical properties of their fluctuations ( etc.).

The largest turbulent eddies interact with and extract energy from the mean flow by a process called vortex stretching

The characteristic velocity and characteristic length of the larger eddies are of the same order as the velocity scale and length scale of the mean flow. This suggests that these large eddies are dominated by inertia effects and viscous effects are negligible. The Reynolds number of the smallest eddies based on their characteristic velocity and characteristic length is equal to 1, , so the smallest scales present in a turbulent flow are those for which the inertia and viscous effects are of equal strength. These scales are named the Kolmogorov microscales.

• Length-scale ratio:
• Time-scale ratio:
• Velocity-scale ratio:

Typical values of might be

We except largest eddies to be highly anisotropic and the smallest eddies in a turbulent flow are isotropic.

Kolmogorov derived the universal spectral properties of eddies of intermediate size, which are sufficiently large for their behaviour to be unaffected by viscous action (as the larger eddies), but sufficiently small that the details of their behaviour can be expressed as a function of the rate of energy dissipation (as the smallest eddies). The appropriate length scale for these eddies is , and he found that the spectral energy of these eddies – the inertial subrange – satisfies the following relationship:

Measurements showed that the constant .

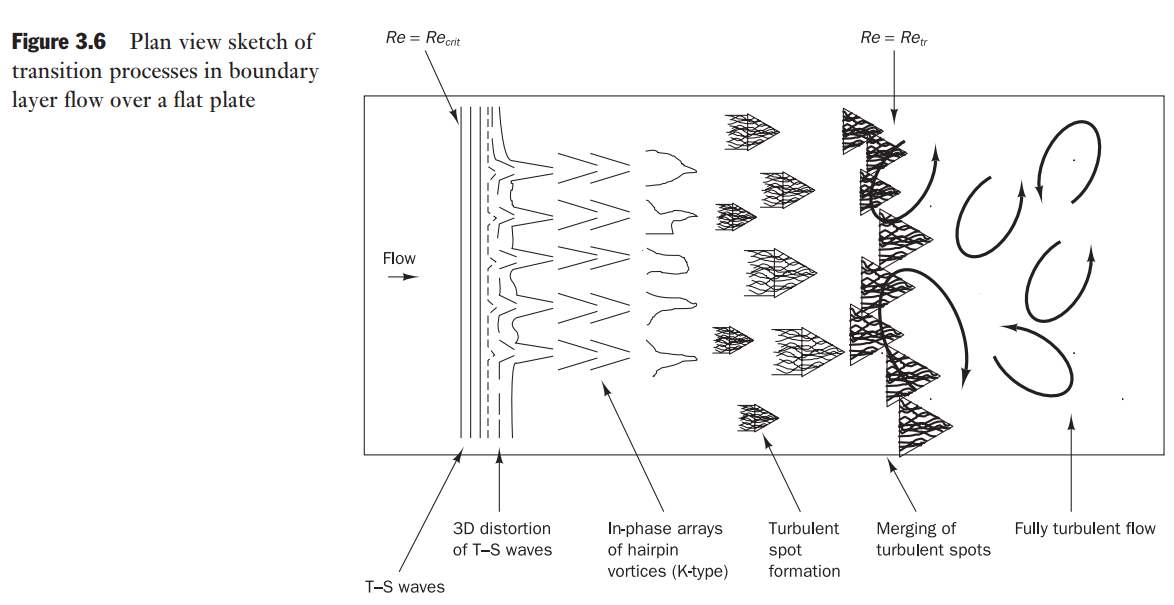
Transition from laminar to turbulent flow

Of particular interest in an engineering context is the prediction of the values of the Reynolds numbers at which disturbances are amplified and at which transition to fully turbulent flow takes place.

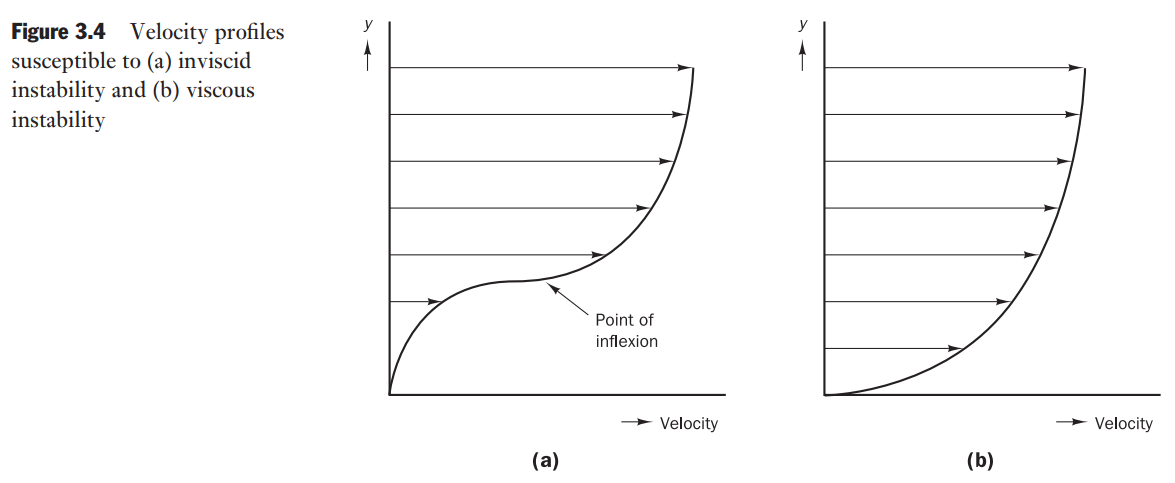
Inviscid instability

• contains a point of inflextion
• associated with jet flows, mixing layers and wakes and also with boundary layers over flat plates under the influence of an adverse pressure gradient .

viscous instability

• without a point of inflextion
• associated with flows near solid walls such as pipe, channel and boundary layer flows without adverse pressure gradients .

Transition to turbulence

Jet flow: an example of a flow with a point of inflexion

Boundary layer on a flat plate: an example of a flow without a point of inflexion

Pipe flow transition

The viscous theory of hydrodynamic stability predicts that these flows are unconditionally stable to infinitesimal disturbances at all Reynolds numbers. In practice, transition to turbulence takes place between and . Various details are still unclear, which illustrates the limitations of current stability theories

Final comments

A number of common features in the transition processes:

1. the amplification of initially small disturbances
2. the development of areas with concentrated rotational structures
3. the formation of intense small-scale motions and finally
4. the growth and merging of these areas of small-scale motions into fully turbulent flows

Descriptors of turbulent flow

• Mean component:
• Fluctuating component:

Time average or mean

Variance, r.m.s. and turbulence kinetic energy

The variance is also called the second moment of the fluctuations.

The total kinetic energy per unit mass of the turbulence at a given location can be found as follows:

The turbulence intensity is the average r.m.s. velocity divided by a reference mean flow velocity and is linked to the turbulence kinetic energy as follows:

Moments of different fluctuating variables

The variance is also called the second moment of the fluctuations. For different fluctuating variables, their second moment:

Higher-order moments

The third and fourth moments are related to the skewness (asymmetry) and kurtosis (peakedness), respectively:

Correlation functions - time and space

More detailed information relating to the structure of the fluctuations can be obtained by studying the relationship between the fluctuations at different times. The autocorrelation function is defined as

Similarly, shifted by a certain distance in space:

Probability density function

Probability density function is related to the fraction of time that a fluctuating signal spends between and .:

The average, variance and higher moments of the variable and its fluctuations are related to the probability density function as follows:

Characteristics of simple turbulent flows

Free turbulent flows:

• mixing layer
• jet flow
• wake
  Boundary layer near solid walls:
• flat plate boundary layer
• pipe flow

Free turbulent flows

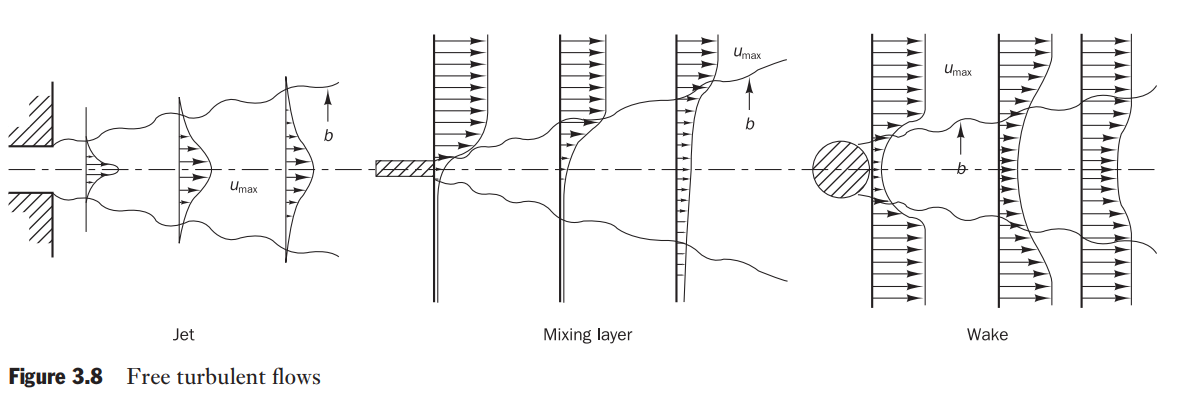
• A mixing layer forms at the interface of two regions: one with fast and the other with slow moving fluid.
• In a jet a region of high-speed flow is completely surrounded by stationary fluid.
• A wake is formed behind an object in a flow, so here a slow moving region is surrounded by fast moving fluid.

The largest values of , and are found in the region where the mean velocity gradient is largest, highlighting the intimate connection between turbulence production and sheared mean flows.

Flat plate boundary layer and pipe flow

• Linear or viscous sub-layer - the fluid layer in contact with a smooth wall
• Log-law layer - the turbulent region close to a smooth wall
• Outer layer - the inertia-dominated region far from the wall

The effect of turbulent fluctuations on properties of the mean flow

Reynolds-averaged Navier—Stokes equations for incompressible flow

Some rules for and :

For a fluctuating vector quantity and a fluctuating scalar :

Now we have the equations:

Replace by , , , and . Derive a little bit and we get the Reynolds-averaged Navier–Stokes equations:

The extra stress result from six additional stresses: three normal stresses



and three shear stresses



These extra turbulent stresses are called the Reynolds stresses.

The normal stresses are non-zero because they contain squared fluctuations. The shear stresses contain second moments associated with correlations between different velocity components, however, are also non-zero in practice due to the structure of the vortical eddies and very large compared with the viscous stresses.

Similarly, the time-average transport equation for scalar :

Turbulent flow equations for compressible flows

stands for the density-weighted averaged or Favre-averaged velocity:

Scalar transport equation: