CUDA编程03: 全局内存、共享内存以及原子函数的合理使用

全局内存的合理使用

在启用了L1缓存的情况下,对全局内存的读取将首先尝试经过L1缓存；如果未命中，则接着尝试经过L2缓存；如果再次未命中，则直接从DRAM读取。—次数据传输处理的数据量在默认情况下是32字节。

全局内存的合并与非合并访问

合并（coalesced）访问指的是一个线程束对全局内存的一次访问请求（读或者写）导致最少数量的数据传输，否则称访问是非合并的（uncoalesced）。

合并度（degree of coalescing）它等于线程束请求的字节数除以由该请求导致的所有数据传输处理的字节数。合并访问对应合并度100%

以下讨论忽略L1缓存，即全局内存 –> L2缓存 –> SM，一次将传输32字节数据。

数据传输对数据地址的要求:在一次数据传输中，从全局内存转移到L2缓存的一片内存的首地址一定是一个最小粒度（这里是32字节）的整数倍。例如，一次数据传输只能从全局内存读取地址为0～31字节、32～63字节、64～95字节、96～127字节等片段的数据。

使用CUDA运行时API函数（如我们常用的cudaMalloc）分配的内存的首地址至少是256字节的整数倍。

1. 顺序的合并访问：

   void __global__ add(float *x, float *y, float *z) {
       int n = threadIdx.x + blockIdx.x * blockDim.x;
       z[n] = x[n] + y[n];
   }
   add<<<128, 32>>>(x, y, z);

   x, y和z是由cudaMalloc分配的全局内存的指针。很容易看出,核函数中对这几个指针所指内存区域的访问都是合并的。例如，第—个线程块中的线程束将访问数组x中第0-31个元素，对应128字节的连续内存，而且首地址一定是256字节的整数倍。这样的访问只需要4次数据传输即可完成。所以是合并访问，合并度为100％。
2. 乱序的合并访问：

   void __global__ add_permuted(float *x, float *y, float *z) {
       int tid_permuted = threadIdx.x ^ 0x1;
       int n = tid_permuted + blockIdx.x * blockDim.x;
       z[n] = x[n] + y[n];
   }
   add_permuted<<<128, 32>>>(x, y, z);

   其中，threadIdx.x ^ 0x1是某种置换操作，作用是将0～31的整数做某种置换（交换两个相邻的数）。第一个线程块中的线程束将依然访问数组x中第0～31个元素，只不过线程号与数组元素指标不完全—致而已。这样的访问是乱序的（或者交叉的）合并访问，合并度也为100％。
3. 不对齐的非合并访问

   void __global__ add_offset(float *x, float *y, float *z) {
       int n = threadIdx.x + blockIdx.x * blockDim.x + 1;
       z[n] = x[n] + y[n];
   }
   add_offset<<<128, 32>>>(x, y, z);

   地址偏置了一位，所以将触发5次数据传输，合并度为4/5 * 100% = 80%
4. 跨越式的非合并访问

   void __global__ add_stride(float *x, float *y, float *z) {
       // 注意这里n的表达式与前面的都不一样
       int n = blockIdx.x + threadIdx.x * gridDim.x;
       z[n] = x[n] + y[n];
   }
   add_stride<<<128, 32>>>(x, y, z);

   第—个线程块中的线程束将访问数组x中指标为0, 128, 256, 384等的元素。将触发32次数据传输，属于跨越式非合并访问，合并度为4/32*100%=12.5%
5. 广播式的非合并访问

   void __global__ add_broadcast(float *x, float *y, float *z) {
       int n = threadIdx.x + blockIdx.x * blockDim.x;
       z[n] = x[0] + y[n]; 
   }
   add_broadcast<<<128, 32>>>(x, y, z);

   第一个线程块中的线程束将一致地访问数组x中的第0个元素。这只需要一次数据传输（处理32字节的数据），但由于整个线程束只使用了4字节的数据，故合并度为4/32×100％=12.5％.这样的访问属于广播式的非合并访问。这样的访问（如果是读数据的话）适合采用第6章提到的常量内存。

例子：矩阵转置

完整代码见 matrix.cu ，这里只列出第一种转置函数：

__global__ void transpose1(const real *A, real *B, const int N) {
    const int nx = blockIdx.x * blockDim.x + threadIdx.x;
    const int ny = blockIdx.y * blockDim.y + threadIdx.y;
    if (nx < N && ny < N) {
        B[nx * N + ny] = A[ny * N + nx];
    }
}

矩阵转置需要读写一块内存，比如A为原矩阵（读），B为转置后的矩阵（写），两者只能有一个是合并访问，另一个必是非合并访问。比如上面的函数transpose1()，对A的访问是合并的，对B的写入是非合并的。

在这种情况下，帕斯卡架构及之后的GPU，将读取操作写成非合并的，写入操作写成合并的，会比另一种方式速度快。这主要是因为编译器能够判断一个全局内存变量在整个核函数的范围都只可读（如这里的矩阵A），则会自动用函数__ldg()读取全局内存，从而缓存数据，缓解非合并带来的影响。

所以，在不能满足读取和写入都是合并的情况下，一般来说应当尽量做到合并地写入。

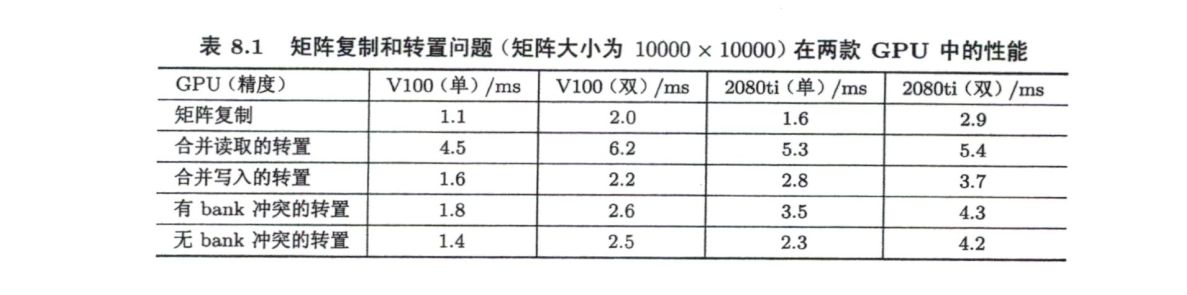
在本人的机器上测试，结果如下：

transpose with coalesced read:
Time = 7.32024 +- 0.531792 ms.

transpose with coalesced write:
Time = 4.16075 +- 0.301832 ms.

transpose with coalesced write and __ldg read:
Time = 4.20045 +- 0.248738 ms.

共享内存的合理使用

共享内存是一种可被程序员直接操控的缓存，主要作用有两个:

• 一个是减少核函数中对全局内存的访问次数，实现高效的线程块内部的通信;
• 另一个是提高全局内存访问的合并度。

例子：数组归约计算

考虑如下简单地对数组求和的函数：

real reduce(const real *x, const int N) {
    real sum = 0.0;
    for (int i = 0; i < N; i++) {
        sum += x[i];
    }
    return sum;
}

考虑一个长度为10⁸的数组，每个元素都是1.23，使用双精度，计算结果为

sum = 123000000.110771

该结果前9位有效数字都正确，从第10位开始有错误。在使用单精度浮点数时，

sum = 33554432.000000

结果完全错误。这是因为，在累加计算中出现了所谓的“大数吃小数”的现象。单精度浮点数只有6、7位精确的有效数字。在上面的函数reduce()中，将变量sum的值累加到3000多万后，再将它和1.23相加，其值就不再增加了（小数被大数“吃掉了”但大数并没有变化）。现在已经发展出更加安全的求和算法，如Kahan求和算法，但这里不讨论。后面会看到，基于CUDA的实现要比上述C＋＋实现稳健（robust）得多，使用单精度浮点数时结果也相当准确。

仅使用全局内存

假设数组元素个数是2的整数次方（这个假设可以轻易去掉），我们可以将数组后半部分的各个元素与前半部分对应的数组元素相加。如果重复此过程，最后得到的第一个数组元素就是最初的数组中各个元素的和。这就是所谓的折半归约（binary reduction）法。

以下为轻易能想到的错误代码：

void __global__ reduce(real *d_x, int N) {
    int n = blockDim.x * blockIdx.x + threadIdx.x;
    for (int offset = N / 2; offset > 0; offset /= 2) {
        if (n < offset) { d_x[n] += d_x[n + offset]; }
    }
}

以上代码问题在于无法保证d_x各个数位的元素被处理的顺序。

可以使用__syncthreads()进行同步。__syncthreads()只同步一个线程块中的所有进程，那么我们就利用该功能让每个线程块对其中的数组元素进行归约。函数代码如下：

void __global__ reduce_global(real *d_x, real *d_y)
{
    const int tid = threadIdx.x;
    real *x = d_x + blockDim.x * blockIdx.x;

    for (int offset = blockDim.x >> 1; offset > 0; offset >>= 1) {
        if (tid < offset) {
            x[tid] += x[tid + offset];
        }
        __syncthreads();
    }

    if (tid == 0) {
        d_y[blockIdx.x] = x[0];
    }
}

• x在不同的线程块中指向全局内存中不同的地址
• 我们这里不再假设N是2的整数次方，但假设N能够被blockDim.x整除，而且假设blockDim.x是2的整数次方（作者采用最常用的线程块大小128）
• 这里我们将blockDim.x / 2写成了blockDim.x >> 1，并将offset /= 2写成了offset >>= 1，这是利用了位操作
• 该核函数仅仅将—个长度为10⁸的数组d_x归约到一个长度为10⁸ / 128的数组d_y。为了计算整个数组元素的和，我们将数组d_y从设备复制到主机，并在主机继续对数组d_y归约，得到最终的结果。这样做不是很高效，但我们暂时先这样做。

使用共享内存

在核函数中,要将一个变量定义为共享内存变量，就要在定义语句中加上一个限定符__shared__，比如：

__shared__ real s_y[128];

• 在一个核函数中定义一个共享内存变量，就相当于在每一个线程块中有了一个该变量的副本。
• 每个副本都不一样，虽然它们共用一个变量名。
• 核函数中对共享内存变量的操作都是同时作用在所有的副本上的。

基于共享内存，可以定义归约函数为：

void __global__ reduce_shared(real *d_x, real *d_y)
{
    const int tid = threadIdx.x;
    const int bid = blockIdx.x;
    const int n = bid * blockDim.x + tid;
    __shared__ real s_y[128];
    s_y[tid] = (n < N) ? d_x[n] : 0.0;
    __syncthreads();

    for (int offset = blockDim.x >> 1; offset > 0; offset >>= 1) {
        if (tid < offset) {
            s_y[tid] += s_y[tid + offset];
        }
        __syncthreads();
    }

    if (tid == 0) {
        d_y[bid] = s_y[0];
    }
}

• 第8行的__syncthreads()用以确保共享内存变量中的数据对线程块内的所有线程来说都准备就绪。
• 共享内存生命周期仅在核函数内，所以在核函数结束之前需要将共享内存中的某些结果保存到全局内存中。

一般来说，在核函数中对共享内存访问的次数越多，则由使用共享内存带来的加速效果越明显。本例使用共享内存加速效果有限，但相比于仅使用全局内存还有两个好处：

• 一个是不再要求全局内存数组的长度N是线程块大小的整数倍
• 另一个是在归约的过程中不会改变全局内存数组中的数据

共享内存的另一个作用是改善全局内存的访问方式（将非合并的全局内存访问转化为合并的），本例并未涉及。

使用动态共享内存

如果在定义共享内存时把数组长度写错了，就有可能引起错误或者降低核函数性能。使用动态共享内存可以减少这种错误发生的概率。

要使用共享内存，首先在调用核函数时写下第三个参数

<<<grid_size, block_size, sizeof(real) * blocksize>>>

其次，在核函数中：

extern __shared__ real s_y[];

这里不能使用extern __shared__ real *s_y，数组不等价于指针

使用动态共享内存和使用静态共享内存在执行时间上几乎无差别，但可以提高程序的可维护性。

使用共享内存处理转置

有bank冲突

基于共享内存，可以对transpose1()函数优化：

__global__ void transpose1(const real *A, real *B, const int N) {
    __shared__ real S[TILE_DIM][TILE_DIM];
    int bx = blockIdx.x * TILE_DIM;
    int by = blockIdx.y * TILE_DIM;

    int nx1 = bx + threadIdx.x;
    int ny1 = by + threadIdx.y;
    if (nx1 < N && ny1 < N) {
        S[threadIdx.y][threadIdx.x] = A[ny1 * N + nx1];
    }
    __syncthreads();

    int nx2 = bx + threadIdx.y;
    int ny2 = by + threadIdx.x;
    if (nx2 < N && ny2 < N) {
        B[nx2 * N + ny2] = S[threadIdx.x][threadIdx.y];
    }
}

• 对A的读取是合并的，这很容易看出来
• 对B来说，写入也是合并的（可以想象成，也是按照x方向先遍历，但是将S的x, y反转了）

在本人机器上测试结果：

transpose with shared memory bank conflict:
Time = 5.5485 +- 0.328543 ms.

比最初的transpose1()要快。

无bank冲突

为了获得高的内存带宽，共享内存在物理上被分为32个（刚好等于一个线程束中的线程数目，即内建变量warpSize的值）同样宽度的、能被同时访问的内存bank。在除开普勒架构外，每个bank的宽度为4字节。共享内存数组中连续的128字节的内容分摊到32个bank的某—层中，每个bank负责4字节的内容。

只要同一线程束内的多个线程不同时访问同一个bank中不同层的数据,该线程束对共享内存的访问就只需要一次内存事务（memory transaction）。当同一线程束内的多个线程试图访问同一个bank中不同层的数据时，就会发生bank冲突。

在核函数tranpose1()中定义了一个长度为32 * 32 = 1024的单精度浮点型变量的共享内存数组，其排列方式如下图所示

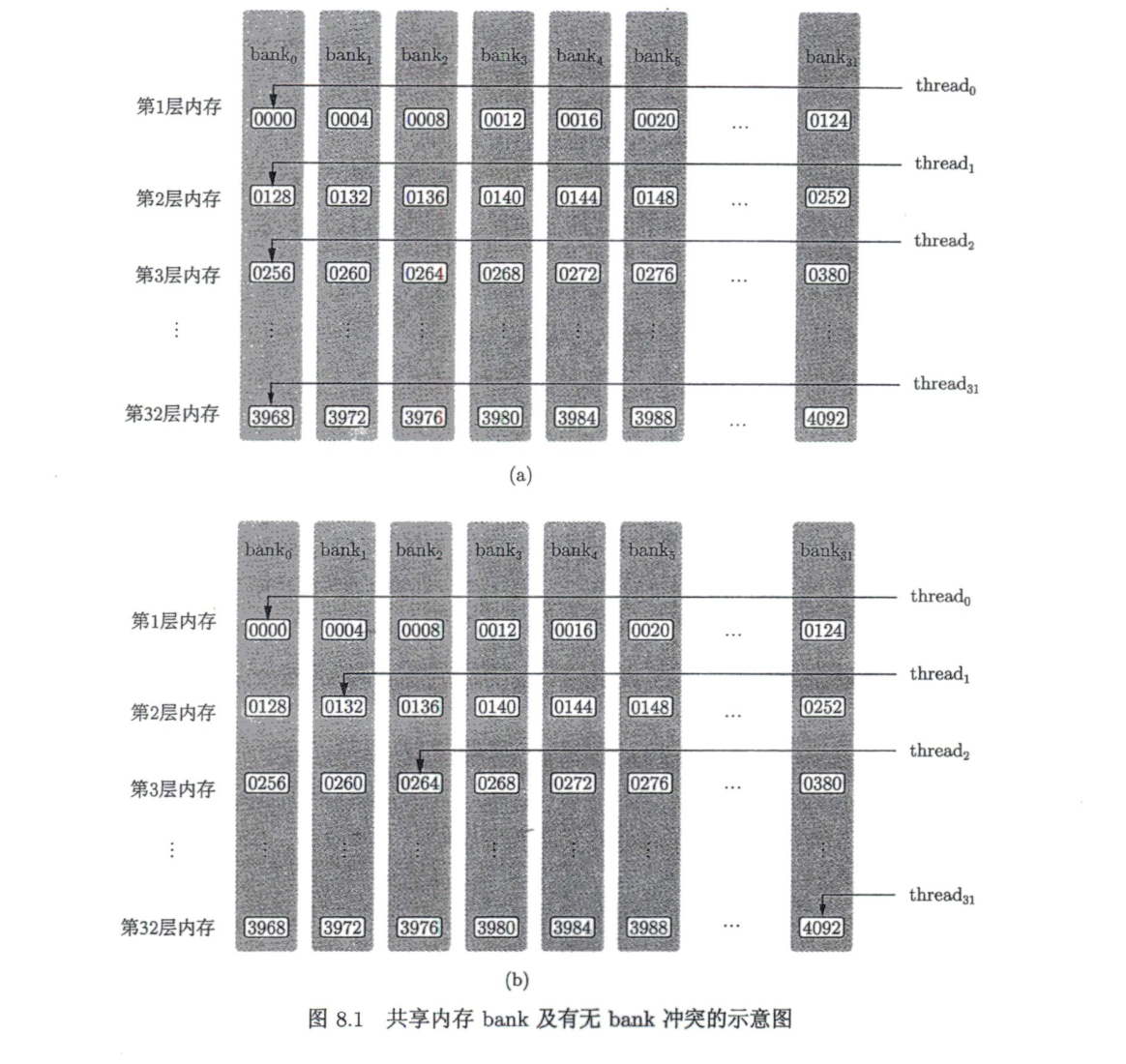
核函数tranpose1()的第16行代码，同一个线程束中的32个线程（连续的32个threadIdx.x值）将对应共享内存数组S中跨度为32的数据。也就是说，这32个线程将刚好访问同一个bank中的32个数据，这将导致32路bank冲突。相比之下，核函数tranpose1()的第9行代码就不会发生bank冲突。

通常可以用改变共享内存数组大小的方式来消除或减轻共享内存的bank冲突。例如，将上述核函数中的共享内存定义修改如下:

__shared__ real S[TILE_DIM][TILE_DIM + 1];

就可以完全消除第16行读取共享内存时的bank冲突。

这里有点不好理解，可以尝试这种思路：二维数组的第二行第一列数据被放在了0132这个位置，0128位置上没有有效数据，那么读取第二行第一列数据时，其实读取的是bank₁第二层内存数据。

在本人机器上测试结果：

transpose without shared memory bank conflict:
Time = 3.51271 +- 0.426474 ms.

作者测试的结果：

原子函数的合理使用

考虑前面数组归约的代码：

void __global__ reduce_shared(real *d_x, real *d_y)
{
    const int tid = threadIdx.x;
    const int bid = blockIdx.x;
    const int n = bid * blockDim.x + tid;
    __shared__ real s_y[128];
    s_y[tid] = (n < N) ? d_x[n] : 0.0;
    __syncthreads();

    for (int offset = blockDim.x >> 1; offset > 0; offset >>= 1) {
        if (tid < offset) {
            s_y[tid] += s_y[tid + offset];
        }
        __syncthreads();
    }

    if (tid == 0) {
        d_y[bid] = s_y[0];
    }
}

如果将最后三行代码改成：

if (tid == 0) {
    d_y[0] = s_y[0];
}

就得不到正确结果，因为线程块之间没有同步，两个线程块可能同时读取d_y[0]。为了克服这个问题，可以才用原子函数：

if (tid == 0) {
    atomicAdd(&d_y[0], s_y[0]);
}

atomicAdd(adress, value)第一个参数是待累加变量的地址，第二个参数是累加的值。该函数的作用是先将地址address中旧值old读出，计算old + val，然后将计算的值存入地址address。原子函数不能保证各个线程的执行具有特定的次序,但是能够保证每个线程的操作一气呵成，不被其他线程干扰，所以能够保证得到正确的结果。完整代码见 reduceGPU_atomic.cu

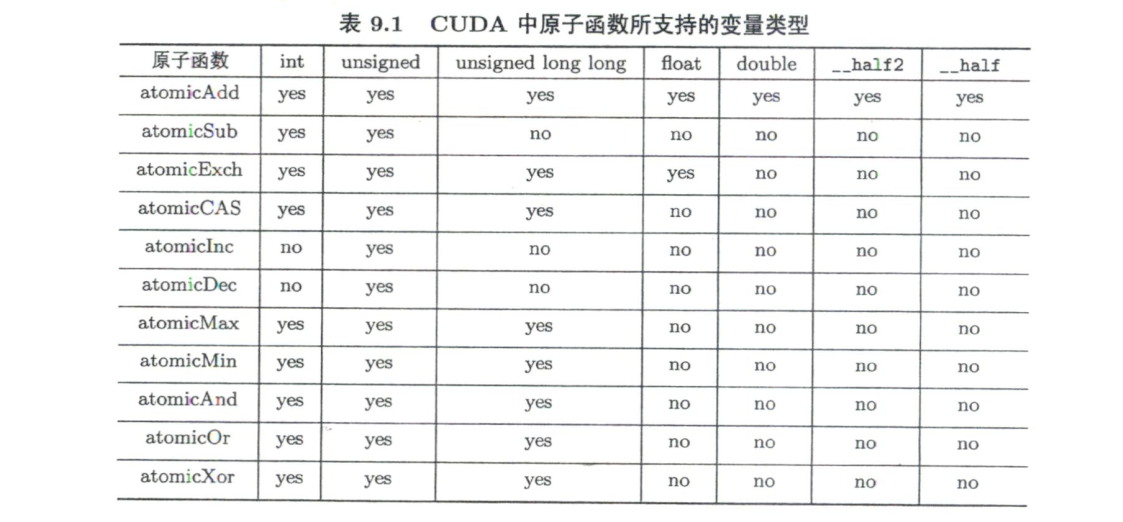
原子函数

原子函数第一个参数可以指向全局内存，也可以指问共享内存。对所有参与的线程来说，该“读-改-写”的原子操作是一个线程一个线程轮流做的，但没有明确的次序。另外，原子函数没有同步功能。

从帕斯卡架构开始，在原来的原子函数的基础上引入了两类新的原子函数。例如，对原子函数atomicAdd()来说，从帕斯卡架构起引入了另外两个原子函数，分别是atomicAdd_system和atomicAdd_block()，前者将原子函数的作用范围扩展到整个同节点的异构系统（包括主机和所有设备），后者将原子函数的作用范围缩小至一个线程块。原子函数的返回值是old

• 加法：T atomicAdd(T *adress, T val);
  功能：new = old + val
• 减法：T atomicSub(T *adress, T val);
  功能：new = old - val
• 交换：T atomicExch(T *adress, T val);
  功能：new = val
• 最小值：T atomicMin(T *adress, T val);
  功能：new = (old < val) ? old : val
• 最大值：T atomicMax(T *adress, T val);
  功能：new = (old > val) ? old : val
• 自增：T atomicInc(T *adress, T val);
  功能：new = (old >= val) ? 0 : (old + 1)
• 自减：T atomicDec(T *adress, T val);
  功能：new = ((old == 0) || (old > val)) ? val : (old - 1)
• 比较-交换：T atomicCAS(T *adress, T compare, T val);
  功能：new = (old == compare) ? val : old
• 按位与：T atomicAnd(T *adress, T val);
  功能：new = old & val
• 按位或：T atomicOr(T *adress, T val);
  功能：new = old | val
• 按位异与：T atomicXor(T *adress, T val);
  功能：new = old ^ val

例子：邻居列表的建立

两个粒子互为邻居的判据如下：它们的距离不大于一个给定的截断距离r_c。

我们的基本算法如下：对每一个给定的粒子，通过比较它与所有其他粒子的距离来判断相应的粒子对是否互为邻居。

这是一个计算量正比于粒子数平方N²的算法，或者算法。对于大体系，有一个更加高效但编程实现相对复杂的算法，计算量仅仅正比于粒子数N，但为简单起见，这里不讨论算法。

原子排列如下图所示：

C++版本：

源代码见 neighborCPU.cu 。寻找邻居的函数如下：

void find_neighbor(int *NN, int *NL, const real* x, const real* y) {
    for (int n = 0; n < N; n++) {
        NN[n] = 0;
    }

    for (int n1 = 0; n1 < N; ++n1) {
        real x1 = x[n1];
        real y1 = y[n1];
        for (int n2 = n1 + 1; n2 < N; ++n2) {
            real x12 = x[n2] - x1;
            real y12 = y[n2] - y1;
            real distance_square = x12 * x12 + y12 * y12;
            if (distance_square < cutoff_square) {
                NL[n1 * MN + NN[n1]++] = n2;
                NL[n2 * MN + NN[n2]++] = n1;
            }
        }
    }
}

• 总原子数N
• 每个原子最多有MN个邻居，这里设为10
• cutoff_square取1.9²
• NN[n]是第n个原子的邻居个数
• NL长度为N * MN，其中NL[n * MN + k]是第n个粒子的第k个邻居
• x和y对应坐标

最后用Python的matplotlib库画出了碳碳键，脚本见 plot_graphene_bond.py ，图如下：

在本人机器上测试，每次运行时间大概在187ms左右（单精度）。

利用原子操作的CUDA版本

从C++修改到CUDA版本，一般首先

• 将线程指标blockIdx.x * blockDim.x + threadIdx.x对应到原子指标n1，去掉循环而改为判断if (n < N)，
• 再修改对n2的循环。

注意不要直接写成：

d_NL[n1 * MN + d_NN[n1]++] = n2;
d_NL[n2 * MN + d_NN[n2]++] = n1;

在与n1对应的线程中，第二条语句代表我们试图对d_NN[n2]进行累加操作。但是，在与n2对应的线程中，第—条语句代表我们也试图对d_NN[n2]进行累加操作，这是不对的。这里应该是原子操作

正确函数应该是：

void __global__ find_neighbor_atomic(
    int *d_NN, int *d_NL, const real *d_x, const real *d_y, const int N, const real cutoff_square
) {
    const int n1 = blockIdx.x * blockDim.x + threadIdx.x;
    if (n1 < N) {
        d_NN[n1] = 0;
        const real x1 = d_x[n1];
        const real y1 = d_y[n1];
        for (int n2 = n1 + 1; n2 < N; ++n2) {
            const real x12 = d_x[n2] - x1;
            const real y12 = d_y[n2] - y1;
            const real distance_square = x12 * x12 + y12 * y12;
            if (distance_square < cutoff_square) {
                d_NL[n1 * MN + atomicAdd(&d_NN[n1], 1)] = n2;
                d_NL[n2 * MN + atomicAdd(&d_NN[n2], 1)] = n1;
            }
        }
    }
}

还需要注意，将原子操作的代码改写成如下形式：

d_NL[n1 * MN + d_NN[n1]] = n2;
atomicAdd(&d_NN[n1], 1);
d_NL[n2 * MN + d_NN[n2]] = n1;
atomicAdd(&d_NN[n2], 1);

是错误的，因为不能保证第二行的原子函数读取的d_NN[n1]有没有被别的线程的原子函数改动过。

不用原子操作的CUDA版本

原子操作会降低并行度。有时可通过改变算法，避免原子操作。对于上面的问题，之所以使用原子操作，是因为不同的线程可能同时写入同一个全局内存地址，从而节省了一般的计算量。如果不节省另一半的计算量，就可以避免使用原子函数。

修改后的程序如下：

void __global__ find_neighbor_no_atomic(
    int *d_NN, int *d_NL, const real *d_x, const real *d_y, const int N, const real cutoff_square
) {
    const int n1 = blockIdx.x * blockDim.x + threadIdx.x;
    if (n1 < N) {
        int count = 0;
        const real x1 = d_x[n1];
        const real y1 = d_y[n1];
        for (int n2 = 0; n2 < N; ++n2) {
            const real x12 = d_x[n2] - x1;
            const real y12 = d_y[n2] - y1;
            const real distance_square = x12 * x12 + y12 * y12;
            if ((distance_square < cutoff_square) && (n2 != n1)) {
                d_NL[(count++) * N + n1] = n2;
            }
        }
        d_NN[n1] = count;
    }
}  

• 这里改变了邻居列表的数据排列方式，将d_NL[n1 * MN + count++]改成了d_NL[(count++) * N + n1]。这是因为n1的变化步调与threadIdx.x一致，这样修改后，对全局内存数组d_NL的访问是合并的。

以上源代码见 neighborGPU.cu 。经本人机器测试，使用原子函数大概耗时1.68ms，不使用原子函数大概耗时1.91ms（均为单精度）。

总结

总的来说，使用原子函数的核函数性能较高。即使使用原子函数能够提升核函数的性能，它还是有一个缺点，即运用原子函数时会引入随机性，因为原子函数只能保证每个原子操作的完整性，并不能保证不同的原子操作之间具有特定的次序。